/**
 * @details: 多项式:a_0 + a_1*x + a_2*x^2 + ... + a_n*x^n的求值
 * @note: 1. 普通从左到右计算
 *        2. 从右到左计算
 * @problems: 1.这两个函数分别执行多少次的加法和乘法运算
 *           2.哪个函数更快
 *          3.这两个函数的CPE分别是多少
 *        4.这两个函数中，为什么第一个函数会运行的比第二个函数快
 */

#include <stdio.h>
#include <stdlib.h>

// 普通从左到右计算
double poly(double a[], double x, long degree)
{
    long i;
    double result = a[0];
    double xpwr = x;
    for (i = 1; i <= degree; i++)
    {
        result += a[i] * xpwr;
        xpwr = x * xpwr;
    }
    return result;
}

// 从右到左计算 (Horner‘s method)
double poly2(double a[], double x, long degree)
{
    long i;
    double result = a[degree];
    for (i = degree - 1; i >= 0; i--)
    {
        result = a[i] + x * result;
    }
    return result;
}

chatgpt 解答

这是一个有趣的问题。虽然直观上认为 poly2（Horner’s method）应该更快，因为它减少了乘法操作的次数，但在实际情况中，poly 的 CPE 更低，运行更快。这种现象可能与现代处理器的架构及编译器优化有很大关系。让我们分析几个原因：

1. 乘法指令的流水线处理

在现代处理器上，乘法和加法指令的延迟不一定是简单的“乘法比加法慢”的情况。很多处理器支持乘法指令的流水线处理，即多个乘法指令可以重叠执行。虽然 poly 每次迭代有两次乘法操作，但处理器可能会通过流水线隐藏这些指令的延迟，使得乘法指令与加法指令同时进行，从而提高性能。

而在 poly2 中，乘法操作 x * result 是一个依赖关系链，每次循环的结果都依赖于上次计算的 result。这导致 poly2 的计算无法充分利用流水线，因为每次迭代需要等待上一次乘法完成才能进行下一次操作，形成“数据依赖”。

2. 分支预测和数据依赖

poly 的计算是线性独立的，每一轮的乘法 a[i] * xpwr 和加法 result += a[i] * xpwr 没有直接的依赖关系，可以独立计算，处理器有更多的机会通过指令级并行化加速计算。而 poly2 中的每一步都依赖于上一次的 result，数据依赖性高，限制了指令并行的优化。

3. 内存访问模式

poly 中的 xpwr 逐步累积，而 poly2 中的 result 依赖于前一个结果。这可能导致 poly2 的操作在寄存器重用上表现较差，处理器需要频繁加载和存储中间结果，增加了内存访问延迟。

4. 编译器优化的影响

不同的编译器和优化级别会对这两个算法的指令调度产生不同的影响。编译器可能会对 poly 做出更有效的优化，尤其是在乘法和加法运算能够被流水线化的情况下。而 poly2 由于其递归式的结构，编译器可能难以进行相同程度的优化。

总结

尽管 poly2 在理论上减少了乘法次数，按理应该更快，但由于处理器架构的复杂性，流水线的使用，数据依赖关系以及编译器优化等因素，poly 实际运行起来反而更快，CPE 更低。

个人总结答案

从这一小节的标题可以得知，我们是了解一下现代处理器的结构和运行流程。我们可以得知：现代处理器是==乱序执行，并行处理==的

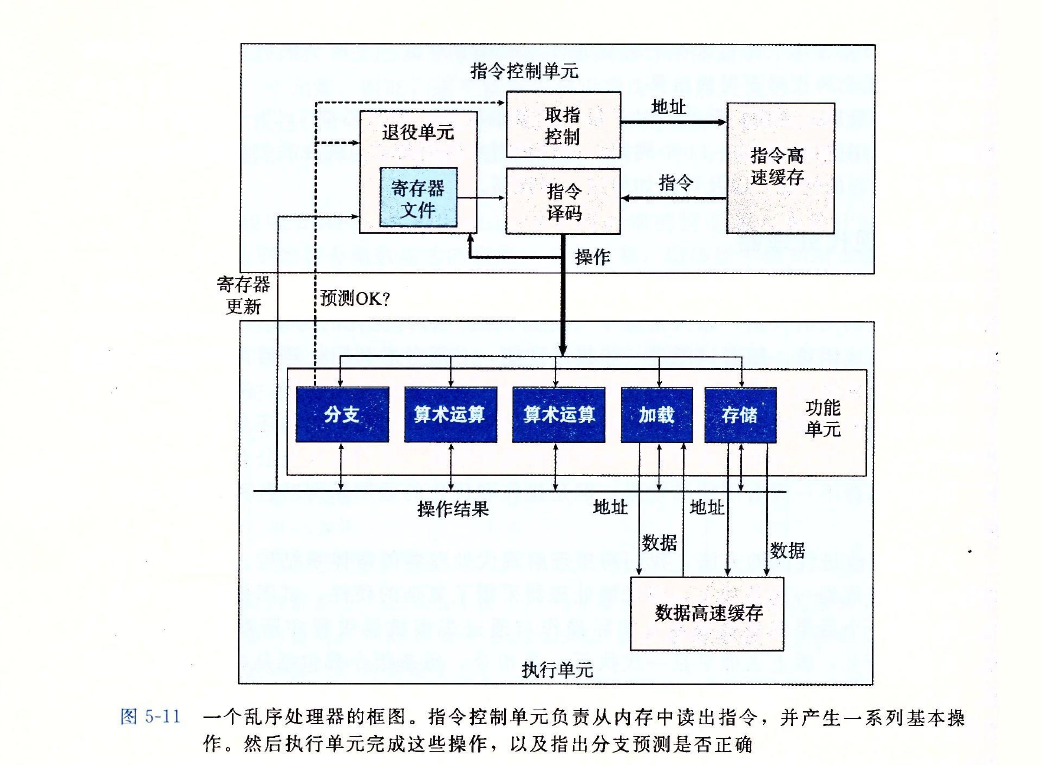
我们写的程序经过编译后得到汇编代码，这个汇编代码算是可以理解为处理器的一个流程吧！可以根据这个过程汇出一个==数据流图==

[!NOTE] 将这一节汇总起来可以说是 ：现代处理器执行能力和计算能力已经还行了。对于多执行命令都可以实现并行乱序执行。从而，上面的代码问题可以总结为：** ploy 函数因为结果的计算没有依赖关系，所以 result 的计算，xpwr 的计算等都可以并行计算。但是，ploy2 函数中下一个 result 的结果依赖于上一个，从而没有充分发挥处理器的优势，没有充分利用流水线的高效率。最终，ploy2 函数快于 ploy**